Ellipse is an elongated form of circle or in other words, circle is an special case of ellipse where the two radii of the circle are equal. Cvc An ellipse explained as a set of points such that the sum of distances from two fixed points (foci) is same for all points given a point P = (x, y), distances are d1 & d2, equation is :
d1 + d2 = constant _ _ _ (1)
In terms of local coordinates
F1 = (x1, y1) & F2 (x2, y2)
Equation is :
_ _ _ (2)
This can also be written in the form :
Ax2 + By2 + Cxy + Dx + Ey + F = 0 _ _ _ (3)
(More A, B, C, D, E, & F are evaluated in terms of focal coordinates & major minor axis).
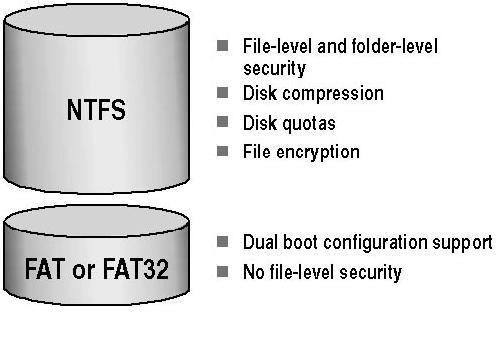
• Major axis – which extends form 1 point to other through foci.
• Minor axis – which spans the shouter dimension bisecting major axis at ellipse center.
An interactive method for specifying an ellipse in an arbitrary orientation is to input two foci & a point on ellipse boundary & evaluate constant in equation (1) & so on.
Equation can be simplified if ellipse is in “standard position” with major & minor axis oriented parallel to x and y axis.
y
yc
xc x
= 1 _ _ _(4)
Now using polar coordinates r & θ
Parameter equations are :
x = xc + rx cos θ
y = yc + ry sin θ